Abstract
Problem
Most existing HIN-based methods rely on explicit path reachability to leverage path-based semantic relatedness between users and items, e.g., metapath-based similarities. These methods are hard to use and integrate since path connections are sparse or noisy, and are often of different lengths.
现有的方法,依赖于物品和用户之间的语义构成的路径,比如metapath的相似度。这些方法在遇到路径很稀少、充满噪音或长度不一致时会导致表示能力的下降。
Other graph-based methods aim to learn effective heterogeneous network representations by compressing node together with its neighborhood information into single embedding before prediction. This weakly coupled manner in modeling overlooks the rich interactions
among nodes, which introduces an early summarization issue.对于图卷积的方法来说,他们只学习了临近邻居的信息,并把他们聚合到一个向量中进行表示,这样很可能导致忽视了一些节点之间复杂的联系。
In this paper, author propose an end-to-end Neighborhood-based Interaction Model for Recommendation to address above problems.
Author first analyze the significance of learning interactions in HINs and then propose a novel formulation to capture the interactive patterns between each pair of nodes through their metapath-guided neighborhoods.
Then, to explore complex interactions between metapaths and deal with the learning complexity on large-scale networks, we formulate interaction in a convolutional way and learn efficiently with fast Fourier transform.
Challenge
- How to tackle the early summarization issue? Due to the complex structure of the HIN, the interactive local structures are hidden and not fully utilized in previous methods.
- How to design an end-to-end framework to capture and aggregate the interactive patterns between neighborhoods? There are usually various nodes in different types involved in one path. Different paths/nodes may contribute differently to the final performance.
- How to learn the whole system efficiently? Learning interactive information on HINs is always time-consuming; especially when faced with paths in different types and lengths for metapath-based approaches and large-scale high-order information for graph-based approaches.
Preliminary
Recommendation:

HIN Graph:$\mathcal{G}=(\mathcal{V},\mathcal{E})$, which consists of more than one node type or link type.
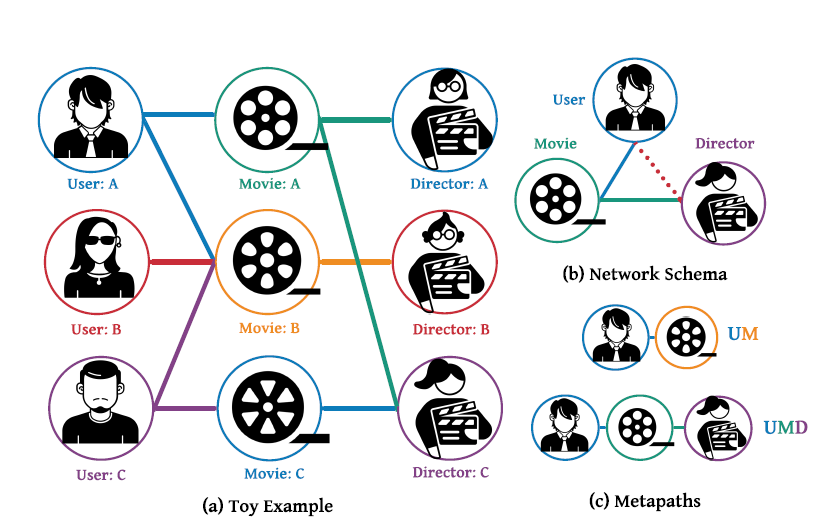
Metapath-guided Neighborhood:Given an object $o$ and a metapath $ρ$ (start from $o$) in an HIN, the metapath guided neighborhood is defined as the set of all visited objects when the object $o$ walks along the given metapath $ρ$.
$\mathcal{N}_p^i(o)$ is the neighbors of object $o$ after $i$-th steps sampling.
$\mathcal{N}_p^0(o)=o$
$\mathcal{N}_p^{I-1}(o)=\mathcal{N}_p(o)$, $I$ is the length of metapath.
$H[\mathcal{N}p(o)]_l=[e^p_0\oplus e^p_1\oplus\cdots\oplus e^p{I-1}]$: The embedding matrix of metapath $\rho$
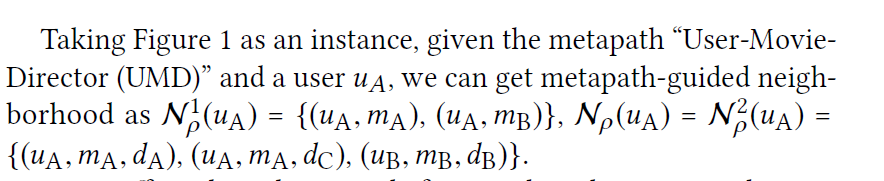
Method
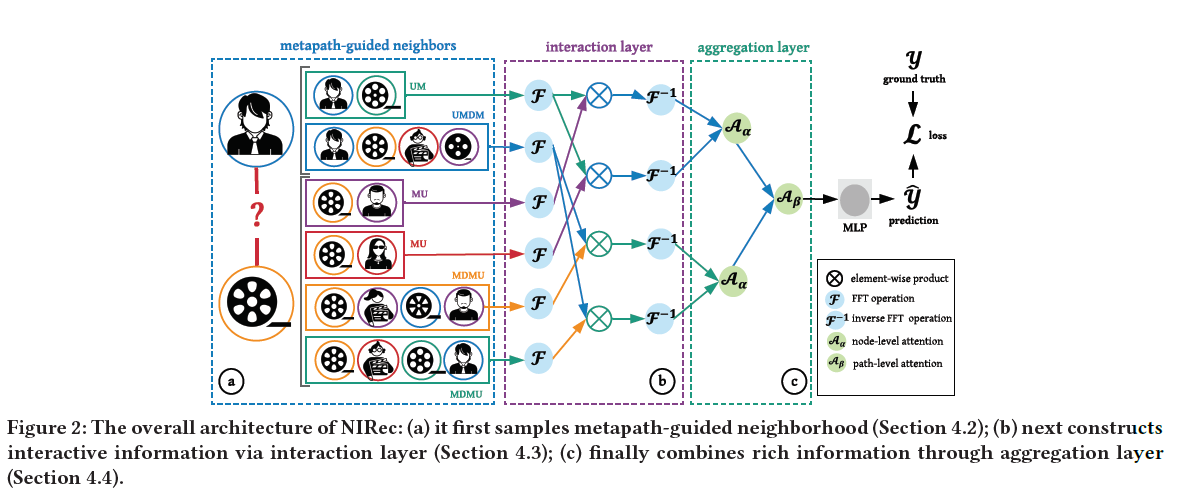
INPUT:
- Select the metapath-guided neighbors for source and target via neighbor samplings.
- Use interactive convolutional operation to generate potential interaction information among the neighbors
- Aggregate information via attentnion mechanism in both node and path level.
OUTPUT: Final prediction
Neighborhood Sampling

Interaction Module
Due to the heterogeneity of nodes, different types of nodes have different feature spaces. Hence, for each type of nodes with type $\phii$. Author design the type-specific transformation matrix $M{\phi_i}$ to project the features of different types of nodes into a unified feature space.
where $e_i$ and $e’_i$ are the original and projected features of node $i$.
Considering that neighbors in different distances to the source/target node usually contribute differently to the final prediction, author divide the sampled metapath-guided neighborhood into several innerdistance and outer-distance neighbor groups.
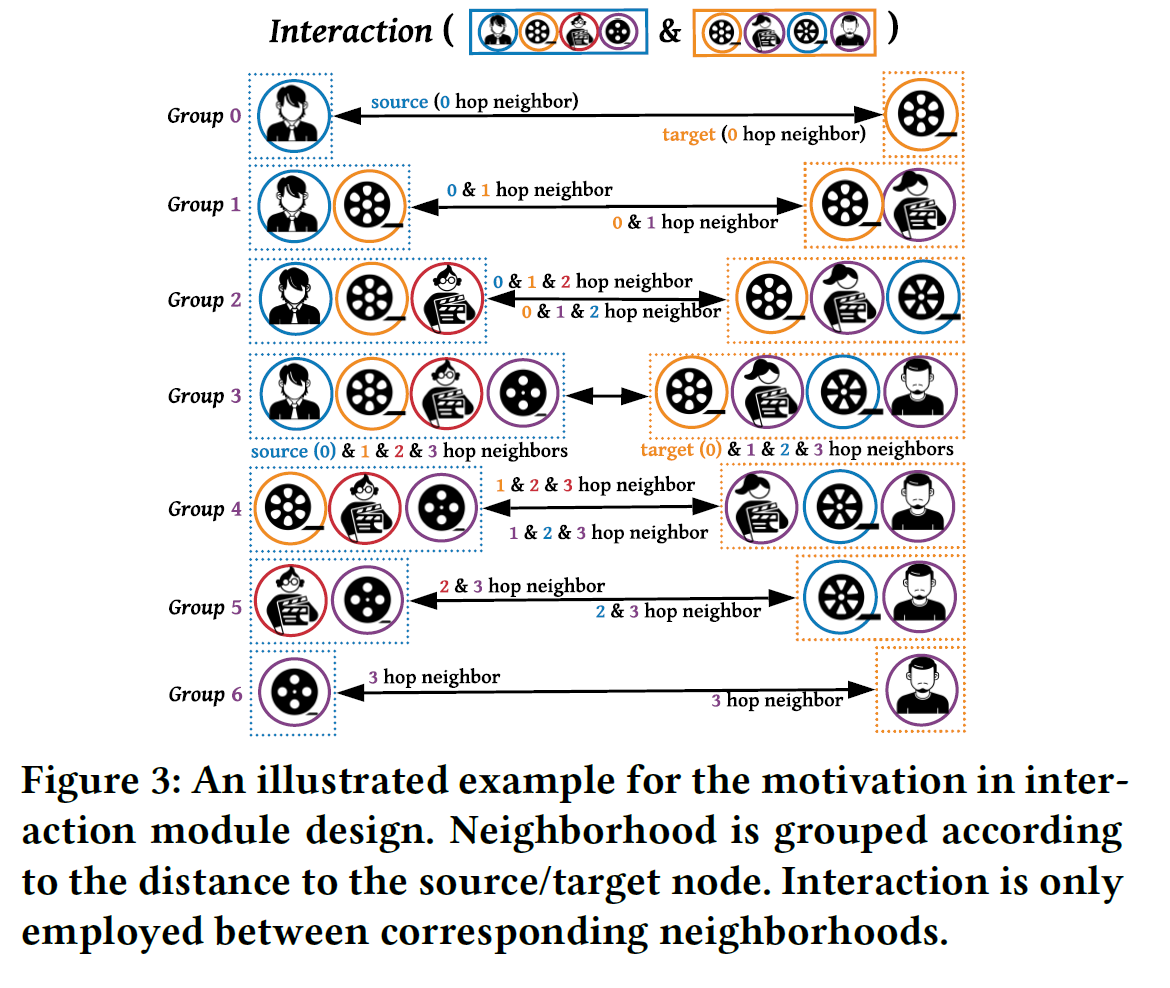
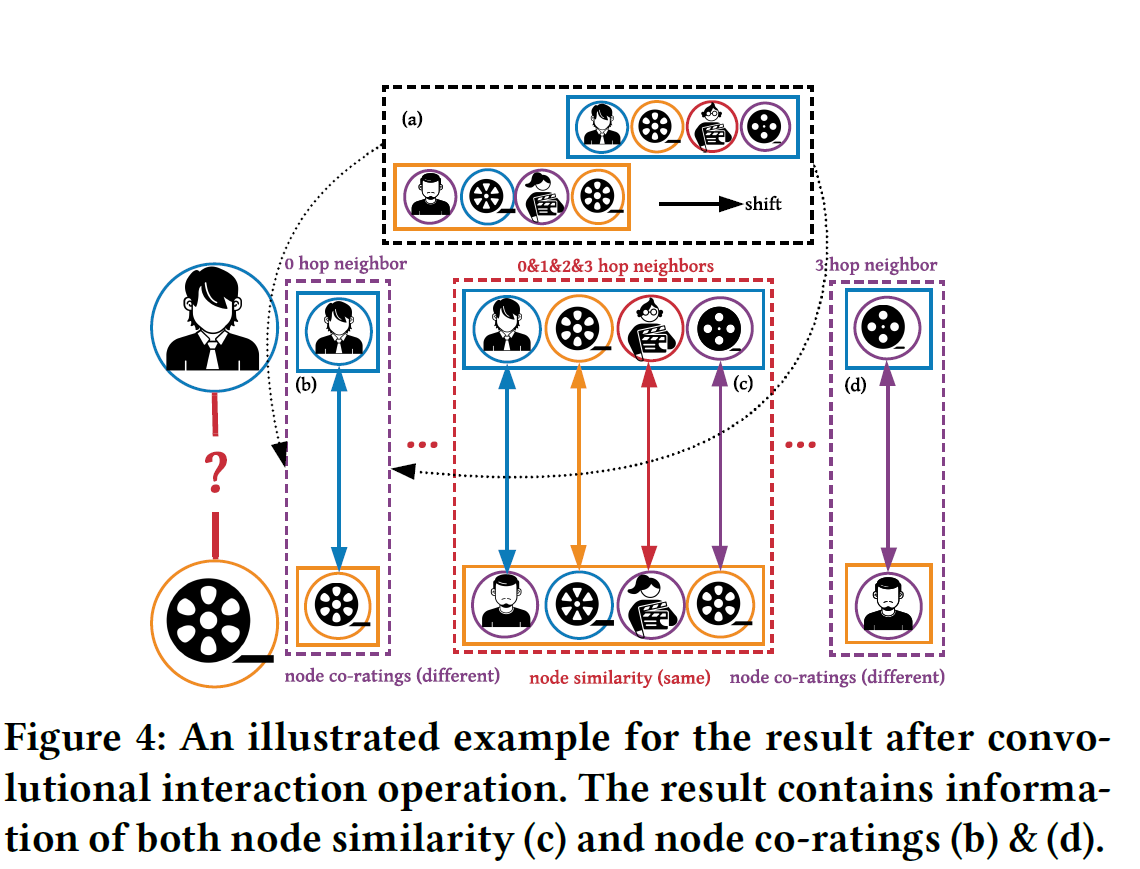
In order to compute the interactions in each neighbor group, author adopt the convolution method:
e.g. calculate the interaction between $u_A,m_B,d_B,m_D$ and $m_B,d_C,m_C,u_C$
- Inverse the order of target movie neighborhood: $u_C,m_C,d_C,m_B$
- Shift the sequence and obtain the co-ratings between different types of nodes like $r(u_A,m_B)$ or $r(u_A,u_C)+r(m_B,m_C),+r(d_B,d_C)+r(m_D,m_B)$by product operation.
Therefore, the above procedure can be written in convolution form:

By using the fast Fourier transformation (FFT) and $\mathcal{F}^{-1}$
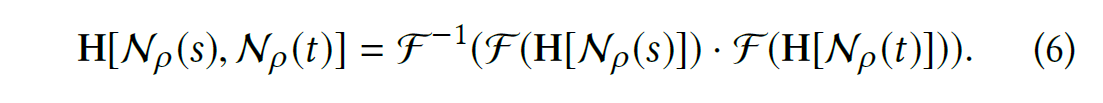
Aggregation Module
Node/Element-level Attention
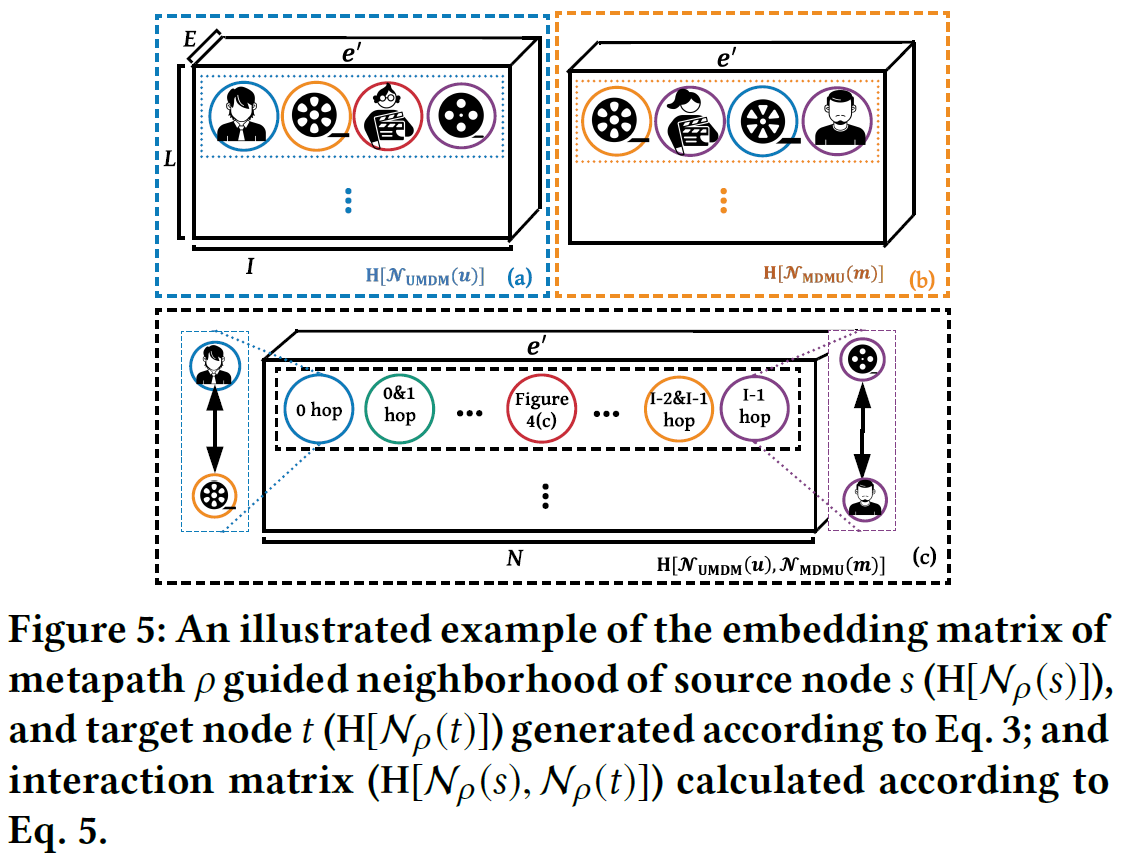
After the interaction module, the author adopt the self-attention to learn the weight among various kinds of nodes in metapath $\rho$
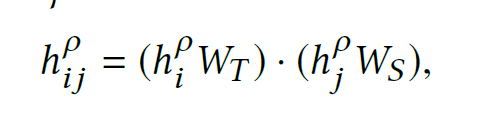
where $h^{\rho}i,h^{\rho}_j$ are elements of interaction matrix $ H[\mathcal{N}{\rho}] $ and $W_T,W_S$ are trainable weights.
The attention value is calculated as bellow
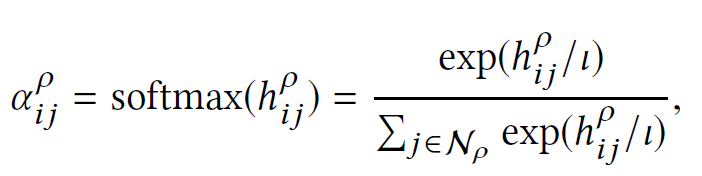
The final result is calculated as:
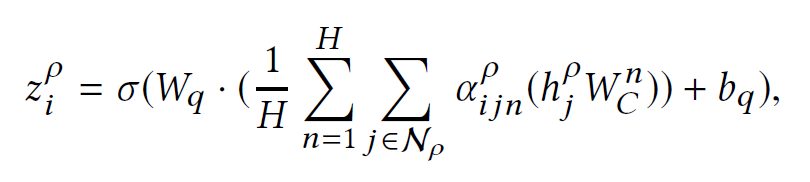
Given a set of metapath $\rho0,\rho_1,\cdots,\rho{P-1}$, we get $Z[\mathcal{N{\rho_0)}}],Z[\mathcal{N{\rho1)}},\cdots,Z[\mathcal{N{\rho_{p-1})}}]$
Path/Matrix-level Attention.
For each metapath aggregate the information with soft attention.

Objective function

Experiment
Five questions

Datasets
Movielens: https://grouplens.org/datasets/movielens/
LastFM: https://grouplens.org/datasets/hetrec-2011/
Result
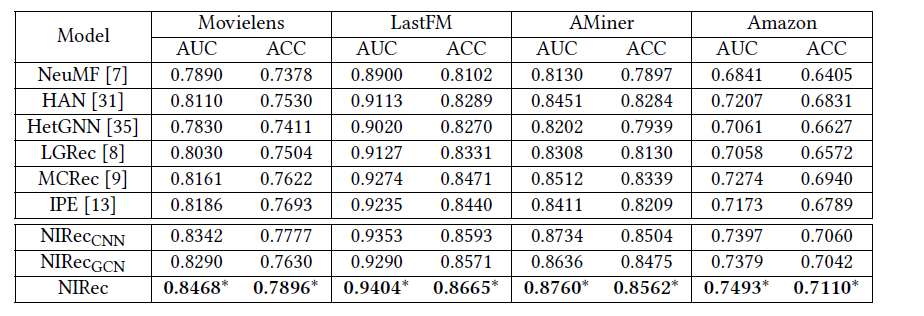
HIRecCNN:Use CNN instead of the interaction module to fuse information around the neighbors.
HIRecGCN:Use GCN instead of the aggregation module to aggregate information from the graph.
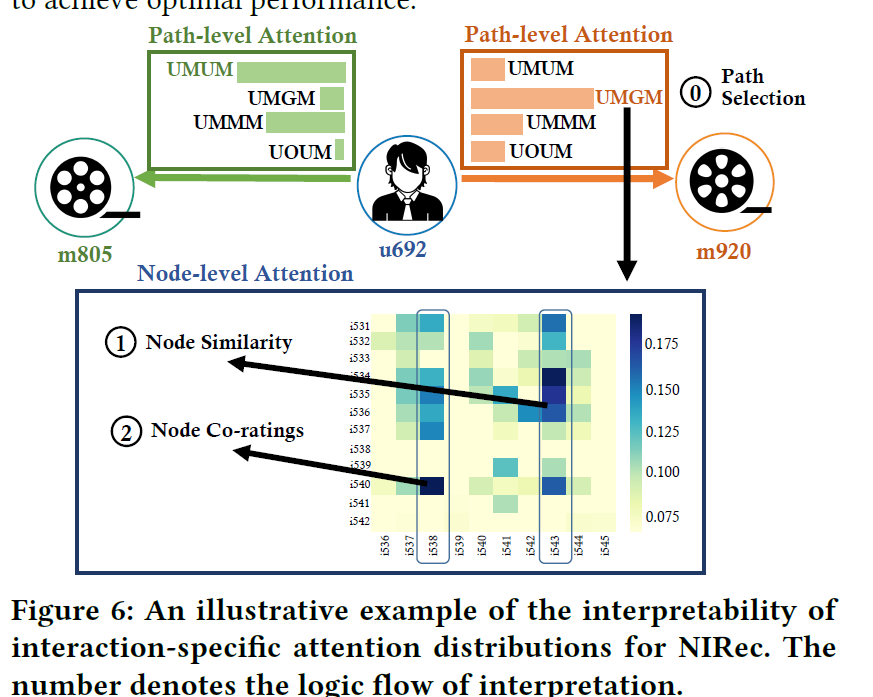
Interpretable
- 显示metapath的重要性
- 显示metapath内部的节点之间的关联关系
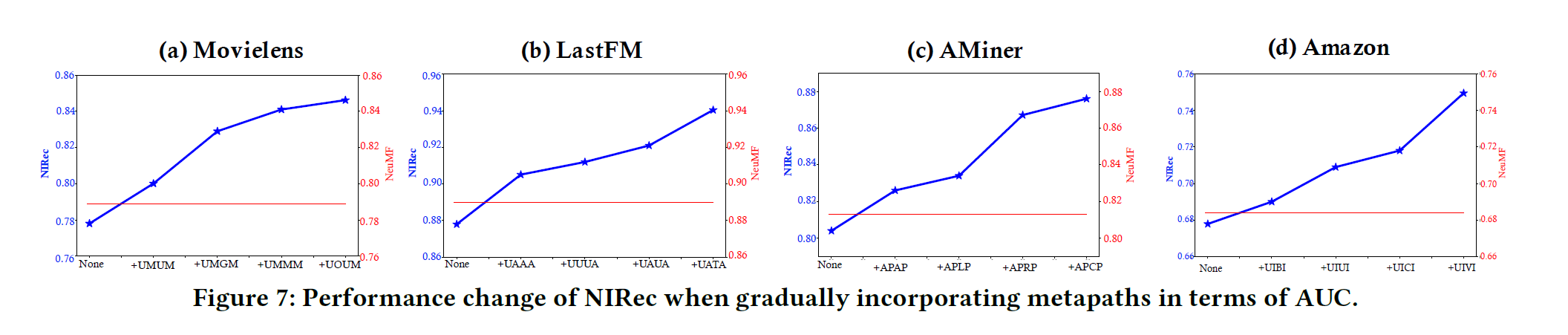
说明增加metapath的对性能的影响
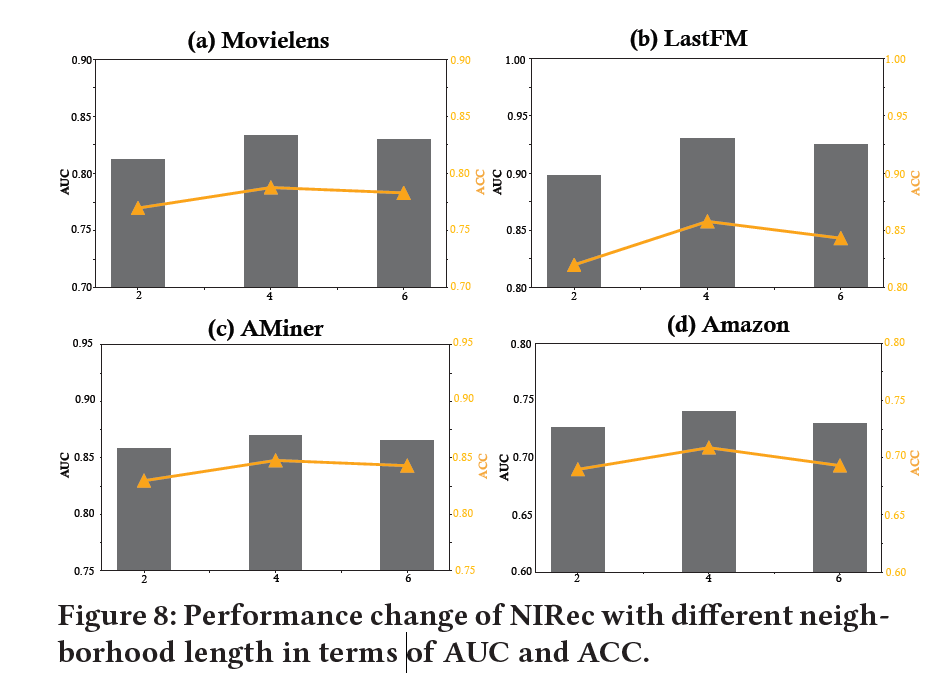
说明邻居长度对性能的影响。