简介：

对一个拥有多种节点重要性的图谱来说，如何去正确的估计他们每个节点重要性是一个很巨大的挑战。其中一个重要的问题就是如何从多种的不同的输入中有效的提取信息。针对这个问题，作者提出了一种隐向量模型，他可以从不同的信号中捕获节点的重要性。

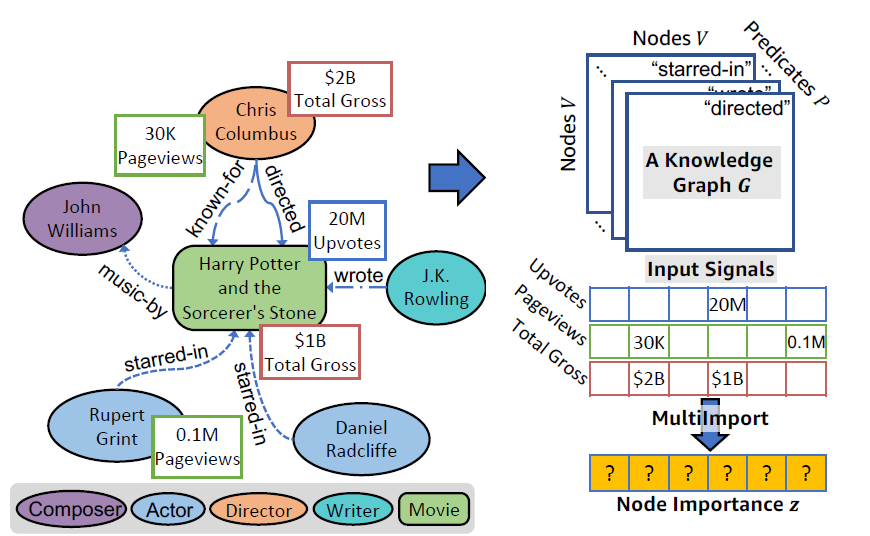
image-20200713103300082

以上图为例，针对一个电影的知识图谱来说，存在不同的种类的的节点，同时每个节点的信息可能拥有不同的属性。以不同的属性作为评价指标，其每个节点的重要性也是不一样的，并且不是每个节点都有全部的属性。这就导致了两个问题：

  1. 节点的重要性以不同的属性作为评价，所得到的结果是不一样的。
  2. 可能会存在空属性的情况，导致节点在那个属性下无法评价重要性。

作者希望对所有节点学习到一个通用的属性重要性$z$，这样作者就可以对图中所有的节点进行一个统一的重要性表达。

符号定义

Node Feature

$X\in \mathbb{R}^{|V|\times F}$

Node Importance

$z\in \mathbb{R}_{\geq 0}$，是一个非负的实数，代表图中每个节点的重要性。

Input Signal

$V’ \to \mathbb{R}_{\geq 0}(V’ \subseteq V)$，同样也是一个重要性，但是一个部分的映射，把一些具有相同属性节点映射到一个重要性空间。对一个数据源，可能有多种不同的signals，比如一本书可以有销售的数量，销售的金额，投票的数量等，所以对一本书的受欢迎的评价可能来自多个不同的方面。同样一些signal只对一些种类的节点有效，所以是一个部分映射。

在本文中，作者设定了$M$个不同的输入signals，${Si: V’_i\to \mathbb{R}{\geq 0}|V’_i \subseteq V,i=1,\dots, M}$

输入的signals有如下的性质：

  • 输入的信号有不同的尺度，可能一个值域是在0-1之间，另一个是在0-100之间。
  • 输入的信号都是值越大节点越重要。

Object Function

我认为本文的目标方程的构建过程是本文最大的贡献点，理论推导严密，合理合规。

给定一个图和一个初始化的参数，目标是学习到一个表达：

为了优化方程$f$，其实就是最大化后验概率

根据贝叶斯理论就是，后验概率等于

证明如下：

$p(\theta)$,是先验参数分布，作者用了中值为0的高斯分布，

$p(\mathcal{G}|\theta)$是用来给定参数$\theta$来表达图的概率。给定一个节点，将其用函数$g(\cdot)$嵌入到低纬空间，然后用KG的triplet来表达图。公式如下：

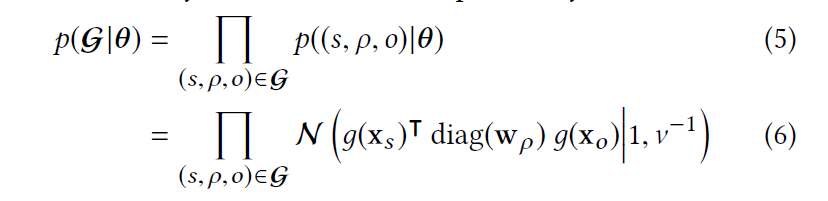
image-20200713141909010

这个公式得到的是每个triplet出现的概率。

$p(S|\mathcal{G},\theta)$是给定一个图和参数，每一个信号出现的概率，其假设学习出的参数，能拟合节点在所有signal里的重要性概率，用极大似然概率，得到如下公式：

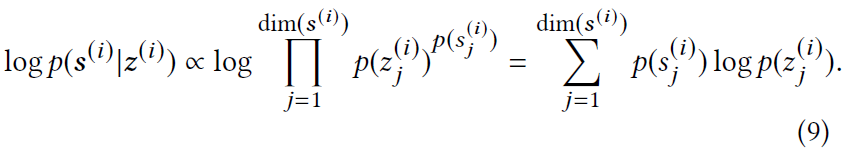
image-20200713142410531

其中$p(s^{(i)}_j)$是，节点在第$i$种signal里的重要性概率，其公式如下:

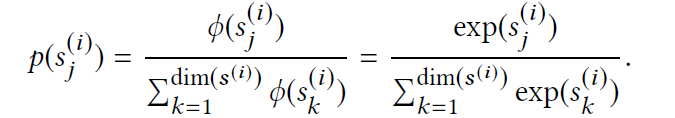
image-20200713142550289

$p(z_j^{(i)})$则是我们学习到的重要性，其表示如下：

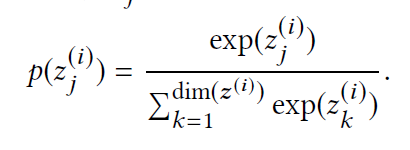
image-20200713142636612

则我们最后得到的目标方程如下：

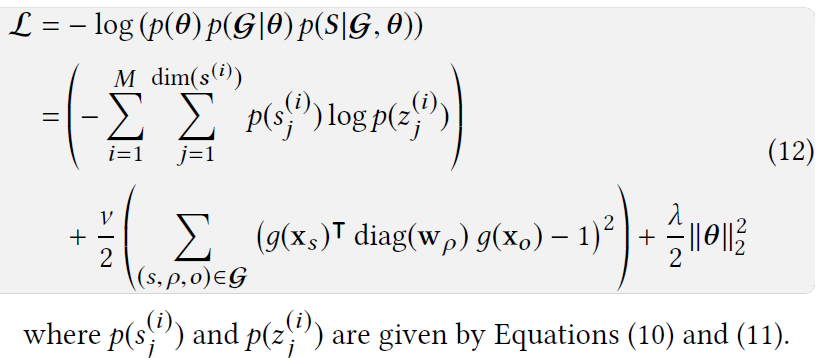
image-20200713142707096

模型和训练过程

节点一开始用函数$g(x)$进行节点嵌入，然后通过$g’(g(x))$（全连接）转换到一维，然后另$h^0=g’(g(x))$

模型在message passing采用的是注意力的加权求和，类似GAT

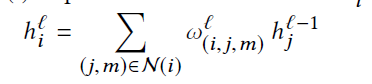
image-20200713142946738

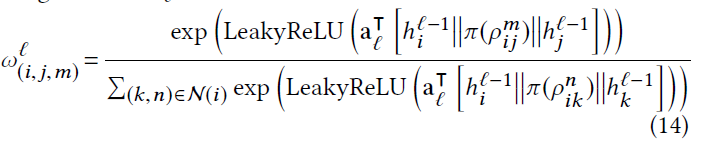
image-20200713143021813

最后对每个节点的表达作者是使用GENI的的中心平均化

最后得到每个重要性的表达向量$z$，注意$z_i$也只是一个值，因为一开始进行了转换。：

image-20200713143538123