简述

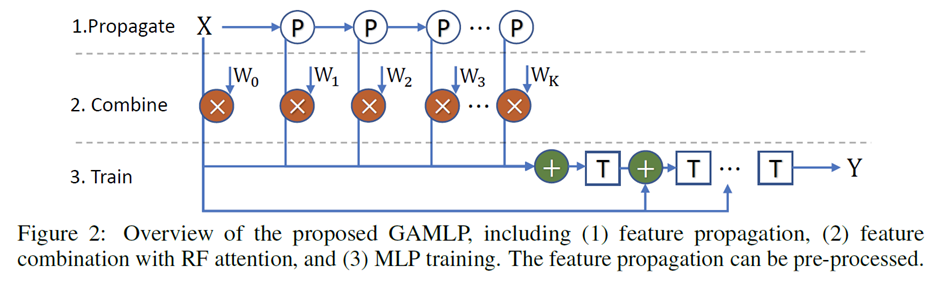
现有的基于半监督的图神经网络算法，不能很好的学习到不同跳的邻居特征。本文提出了一种可以重复的表达不同距离的邻居用户特征的算法。

原始GCN不同层卷积都用相同的权重，不能捕获不同层的信息差异性，本文证明了对不同层采用不同的信息传递权重能捕获不同层之间的信息差异性。

image-20200712155849920

贡献

  1. 提出了Delta Operators，并证明了传统的GCN模型没有能学到这样的表达
  2. 提出了MixHop，通过利用多次邻接矩阵，作者证明MixHop能够学习到更广泛的邻居特征，同时也不会增加模型的内存。

问题

  1. 传统GNN一次只能卷积一次邻居
  2. 在降低邻接矩阵求特征值的复杂度之后丢失了一些信息

假设

image-20200701164504476

模型

image-20200701164046322

Delta Operation

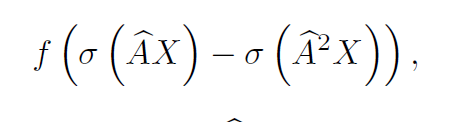
image-20200712163255272

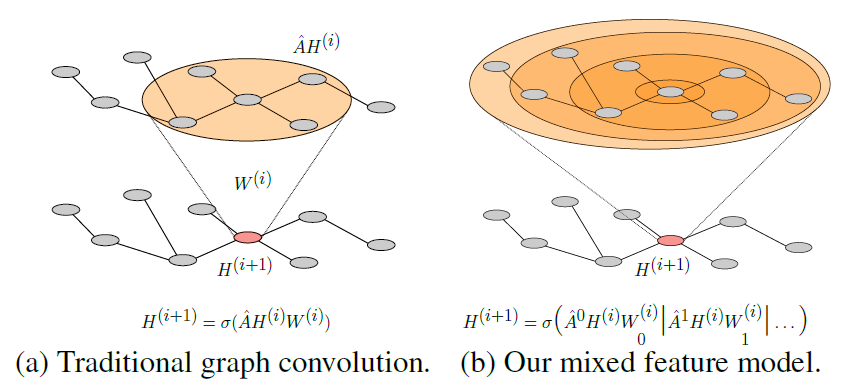
这是一个在不同距离的节点特征之间收集特征的操作。一个模型能够学习到两跳的信息的前提是其存在一组参数和一个injective mapping $f$，可以使得网络的输出可以给定任何邻接矩阵$A$和特征$X$。

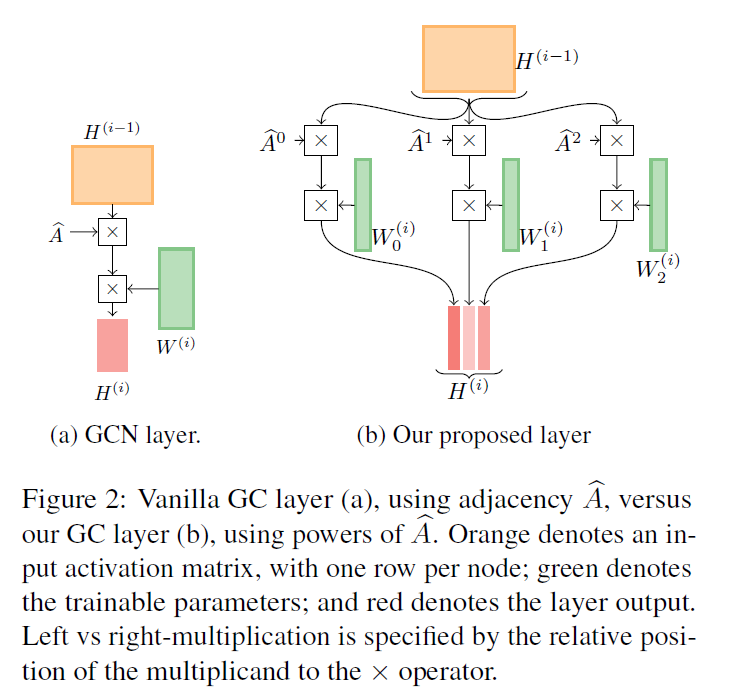
MixHop Graph Convolution Layer

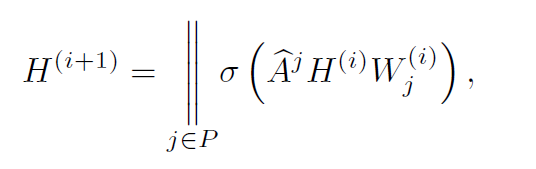
image-20200712174307445

和传统GCN重复乘以A不同，本文在一次操作里乘多次A，一次性获得多跳的信息。并且和传统GCN的每层权重矩阵W相同不一样，这里每一跳都有各自的权重矩阵W。最后将其拼接起来。

模型的表示能力

证明1：传统GCN不能表达two-hop Delta Operators

通过构造$C{1,2}$来证明$W^$是任意两行都是相等的，从而证明$AW^$的rank为1，又证明$AW^*=f$，从而$f$不可能是injective（单射）的，因为任意两行相等，所以对多个不同的两行的$C{xy}$都产生相同的输出。

image-20200712215522230

image-20200712215535565

证明2：证明MixHop具有two-hop性质

通过拼接操作，再加上合理构造的$W$，可以产生two-hop形式的函数。因此可以证明构造的方式是合理的，能捕获two-hop性质。

image-20200712221022566

模型参数

作者针对不同层的$W$，认为不同层的信息重要程度是不一样的，于是作者先用统一的特征维度n进行预训练。然后再训练完之后通过L2正则化，和阈值筛选出新的维度大小，然后再重新训练。通过这个操作，作者认为能表现出不同hop特征的重要程度（这难道不是一个attention就能解决的吗？？）

image-20200712224115002