GHashing Semantic Graph Hashing for Approximate Similarity Search in Graph Databases

Objection：

• Retrieve graphs from the database similar enough to a query.

• • Optimize the pruning stage.

Background:

• Graph Edit Distance (GED) is a method to measure the distance between two graphs.
• The current similarity search, first compute the lower bound between the query and the every candidate graph and they prune the graph larger tan than the threshold. Then, they compute the exact GED in the remaining graphs.

Challenges:

• The computation of Graph Edit Distance (GED) is NP-hard.

• Existing methods cannot handle the large databases due to their exact pruning strategy.

• • Subgraph isomorphism check to generate the graph index
  • GED lower bounds are too loose, which leads to many candidates.

Deep hash retrieval:

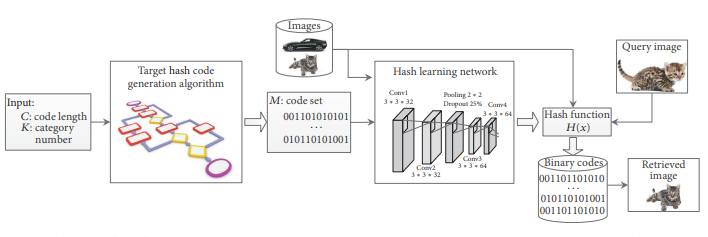
Graph Deep Hash:

• Train a GNN as hash function to generate the index of the graph, where the similarity computation can be done on the hash index instead of the whole graph.
• Prune the graphs using the hash code and embeddings.
• Compute the exact GED using GED solver.

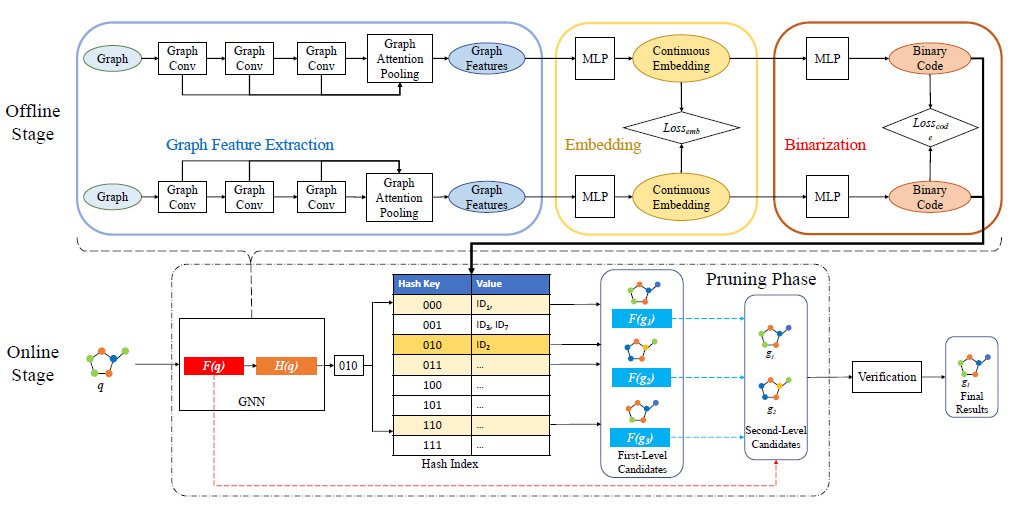
Challenges for Graph Deep Hash:

• The threshold for graph similarity search may vary from query to query, it is appropriate to treat it as a regression problem, which requires estimating GED by hamming distance.
• How to establish a relationship between hamming distance and GED is a problem.
• Lack of positive samples.

Contribution

• We provide a first attempt to use a neural-network-based approach to address the similarity search problem for graph databases via graph hashing.
• We propose a novel method GHashing, a GNN-based graph hashing approach, which can automatically learn a hash function that maps graphs into binary vectors, to enhance the pruning-verification framework by providing a fast and accurate pruner.
• We conduct extensive experiments to show that our method not only has an average F1-score of 0.80 on databases with 5 million graphs but also on average 20× faster than the only state-of-the-art baseline on million-scale datasets.

Preliminaries

•Graph Edit Distance (GED): $ged(g_1,g_2)$ is defined as the minimum number of edit operations to make $g_1$ isomorphic to $g_2$. The operation can be one of the following:

1. Insert a node
2. Delete a node
3. Change the label of the node
4. Insert an edge
5. Delete an edge

Graph Similarity Search under GED: Given a graph database $D$ with $N$ graphs, and a query graph $q$ and a threshold $τ$, the graph similarity search under GED measure aims to find ${g│g∈D∧ged(g,q)≤τ}$

Approach:

Hash function :

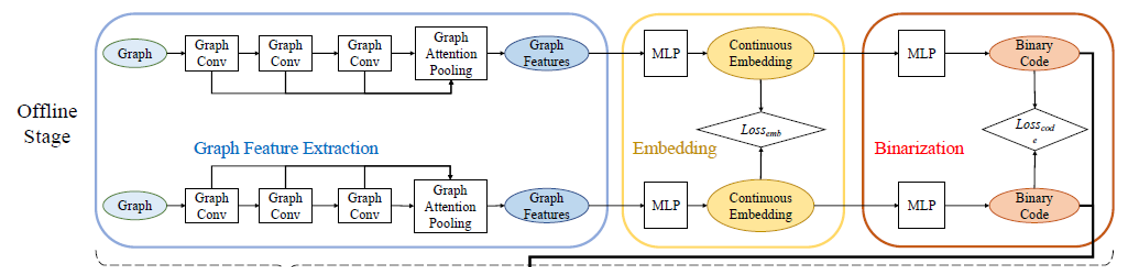
Graph neural network:

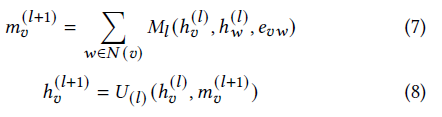
Graph pooling:

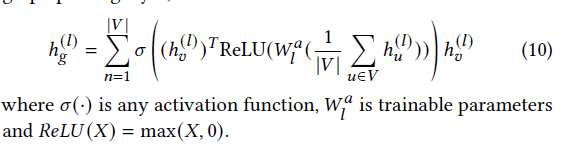
Loss function:

$$L=λL_{code} (g_1,g_2 )+(1-λ) L_{emb} (g_1,g_2 )$$ $$L_{code} (g_1,g_2 )=L(\hat y,y)$$ $$\hat {𝑦} =|𝐻(𝑔_1 )−𝐻(𝑔_2 )|, 𝑦=𝑔𝑒𝑑(𝑔_1,𝑔_2 ), 𝐿 can be any loss function for regression.$$

Design of $L_{code}$

• GED can be arbitrarily large, the hamming distance between two B-bit hash codes can not be larger than B.
• Therefore, L should satisfy following properties:
  • Small punishment when both values are large $L(\hat y,y)=L′(min⁡{γ,\hat y},min{γ,y})$
  • Asymmetric: $L(\hat y,y)≠L(y,\hat y)$, estimated hamming distance should smaller than GED.
  • Minimized when $\hat y= y$
  • Convex

Handling discrete constraints

Hamming distance to Euclidean space

Binary regularization

Design of $L_{emb}$

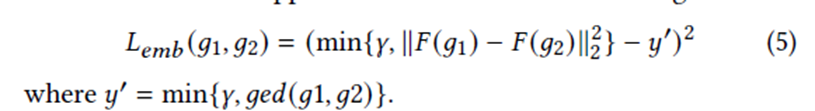
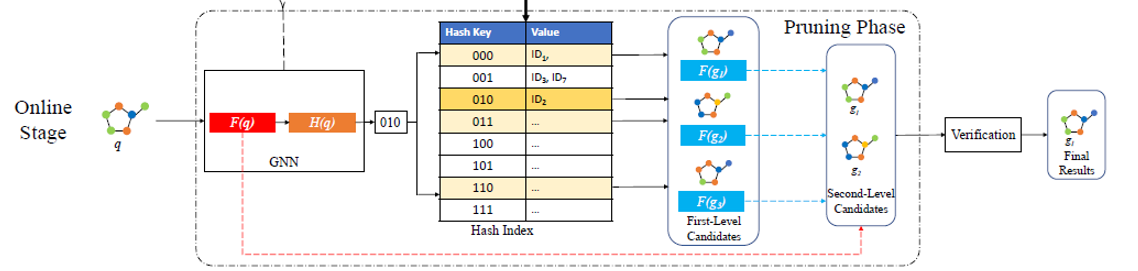
Online Stage

1. Encode the query graph to $H(q)$

2. Search the keys whose hamming distance to $H(q)$ is less than $τ+t$, $t$ is set to 1.

3. Second-stage pruning by computing$||F(g)-F(q)||_2^2>τ+0.5$

4. Verify every graph remained with exact verification algorithm

Experiment:

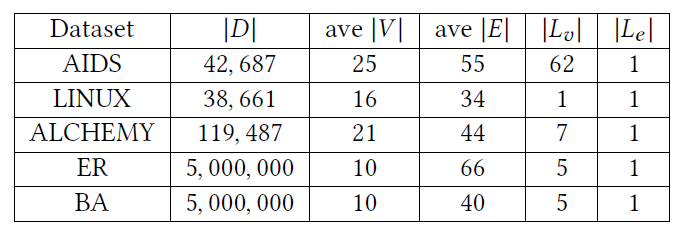
Datasets

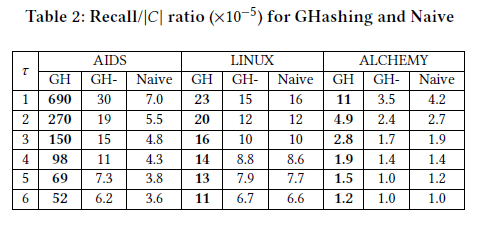
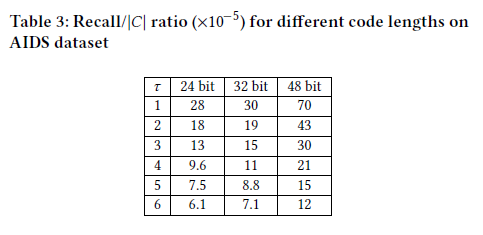
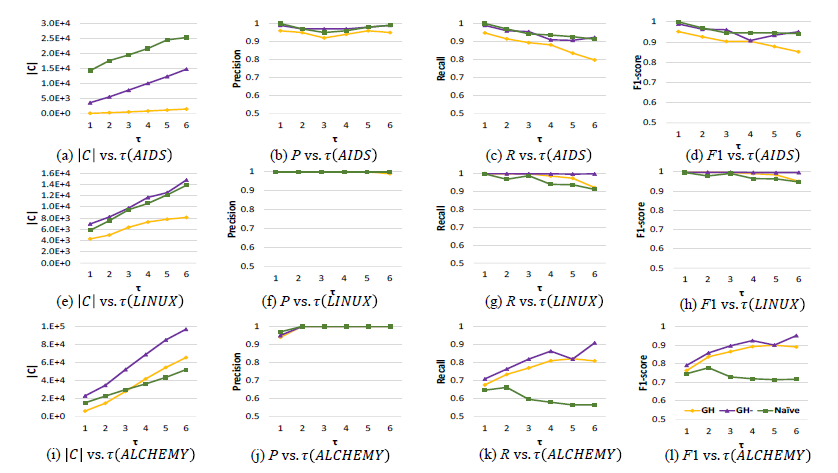
为什么$\tau$越大recall反而下降了呢？

在问了老师之后，可能的解释是随着$\tau$上升，正例的样本也变多了，所以recall下降了。

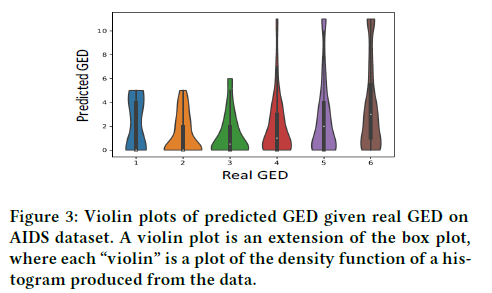
The results in Figure 3 show that the hamming distance is usually smaller than the real GED

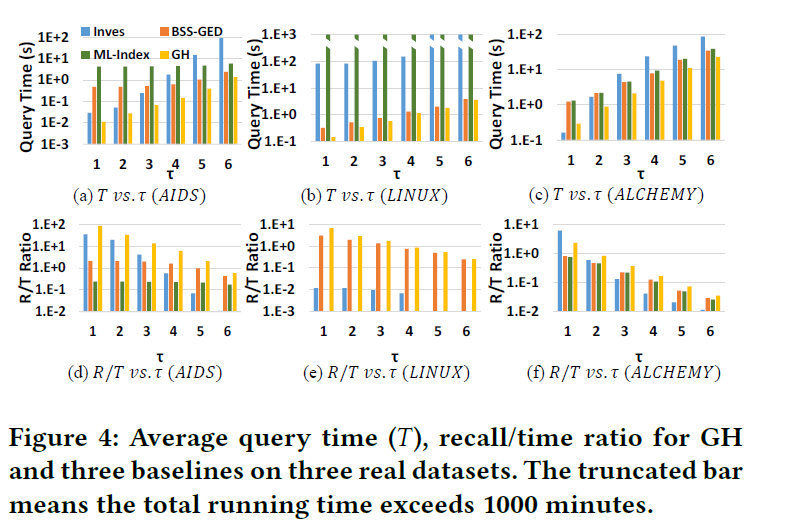
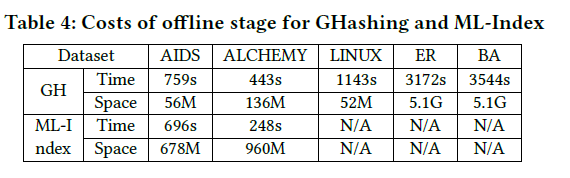
在线查询快，recall高，offline训练时间少，存储空间少。好就完事了！yizhou Sun 牛！