Heterogeneous Deep Graph Infomax
Abstract
Inspired by the emerging mutual information-based learning algorithm, This paper propose an unsupervised graph neural network Heterogeneous Deep Graph Infomax (HDGI) for heterogeneous graph representation learning.
Author utilized the meta-path to model the structure information involving semantics in Heterogeneous graph and apply the graph convolution module and semantic-attention module to capture the individual node local representation.
By maximizing the local-global mutual information, HDGI effectively learns highlevel node representations based on the diverse information in heterogeneous graphs
Unsupervised graph representation learning
- Matrix factorization: capture the global graph information by factorizing the affinity matrix, which ignore the node attributes and local neighborhood relationships.
- Edge-based method: capture the local and high-order neighborhood information by edges connections or random-walk paths, which only preserve limited order node proximity and lack a mechanism
to preserve the global graph structure. - DGI(Deep graph infomax): maximizes the mutual information between graph patch representations and the corresponding high-level summaries of graphs. It has shown competitive performance even compared with supervised graph neural networks in benchmark homogeneous graphs.
Contribution
- This paper presents the first model to apply mutual information maximization to representation learning in heterogeneous graphs.
- HDGI, is a novel unsupervised graph neural network. It handles graph heterogeneity by utilizing an attention mechanism on meta-paths and deals with the unsupervised settings by applying mutual information maximization.
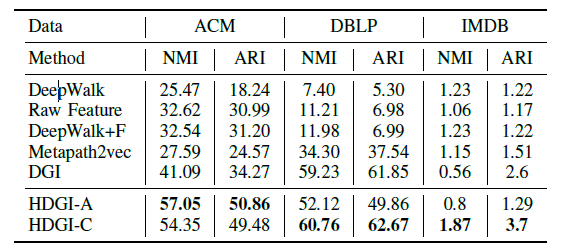
- HDGI are effective for both node classification and clustering tasks. Moreover, its performance can also beat state-of-the-art GNN models, where they have the additional supervised label information.
Mutual information
Mutual information is a quantity that measures a relationship between two random variables that are sampled simultaneously.
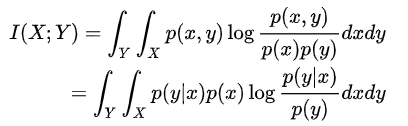
In order to maximize the MI, we need maximize the $\frac{p(y|x)}{p(y)}$, which means $p(y|x)$ is bigger than $p(y)$. For each input $x$, the encoder can find a feature $y$ that can well represent $x$.
Notation
Heterogenous graph: $\mathcal{G}=(\mathcal{V},\mathcal{E})$
Node type mapping function: $\phi:\mathcal{V}\to\mathcal{T},\phi(v)\in \mathcal{T}$
Edge type mapping function:$\psi:\mathcal{E}\to\mathcal{R},\psi(e)\in \mathcal{R}$
$\mathcal{T}+\mathcal{R}>2$
Metapath: $\Phi=v1 \mathop{\to}\limits^{R_1}\cdots \mathop{\to}\limits^{R{n-1}}v_n$
Given a metapath $\Phii$, if there exists a metapath instance between $v_i,j_j$, then $A{ij}^{\Phi_i}=1$ where $A^{\phi_i}$ is the adjacent matrix of metapath $\Phi_i$.
Problem definition: Given a $\mathcal{G}$ and the initial feature matrix $X$, the representation $H\in\mathbb{R}^{|V|\times d}$ which contains both structure and node attributes information.
Approach
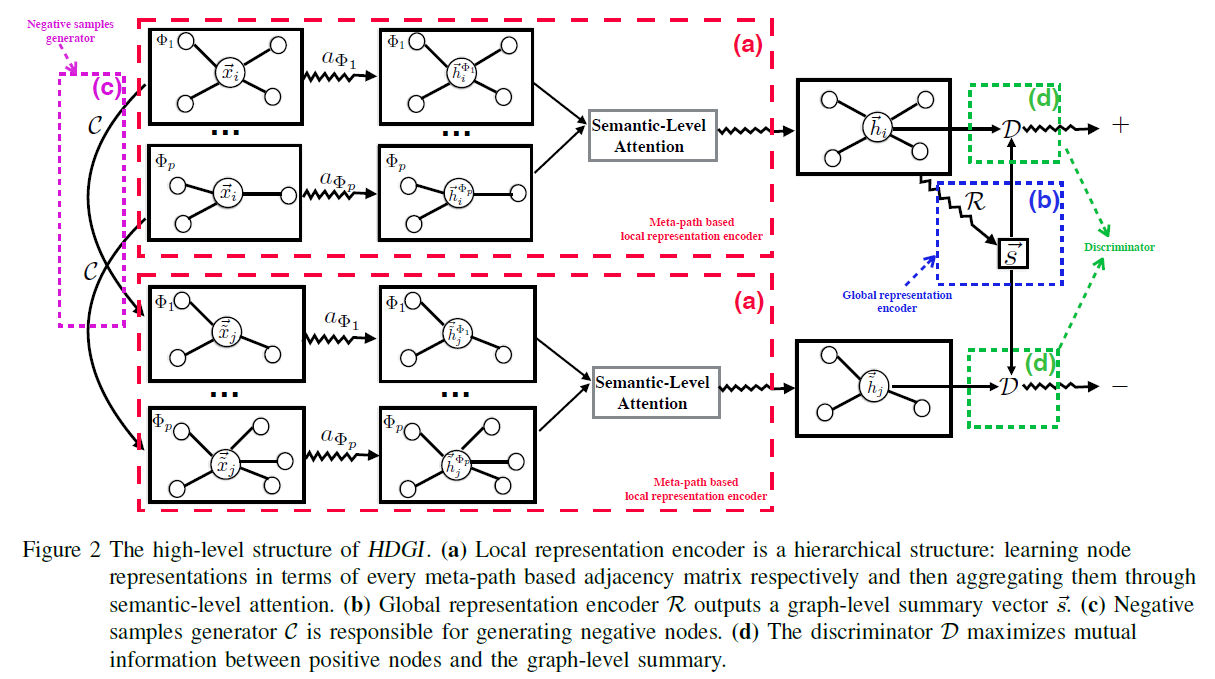
Meta-path based local representation encoder
The first step is meta-path specific node representation learning which encodes nodes in terms of each meta-path based adjacency matrix respectively.
Two kinds of encoder are considered in this work.
GCN:
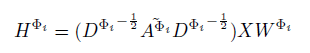
Where $A^{\widetilde{\Phi_i}}=A^{\Phi_i}+I$
GAT:
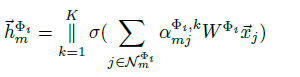
Heterogeneous graph node representation learning
After the meta-path representation, We need to aggregate the more general representations of the nodes.
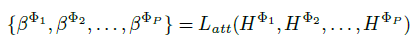
The importance of each meta-path is calculated as:
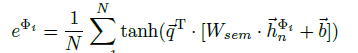
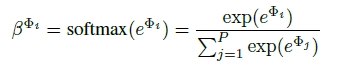
The final representation $H$ is obtained by:
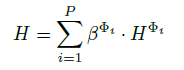
Global Representation Encoder
Averaging encoder function.
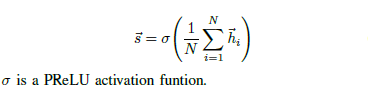
Pooling encoder function
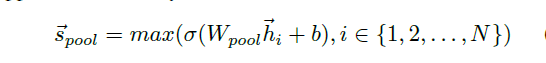
Each node’s vector is independently fed through a fully connected layer. An elementwise max-pooling operator is applied to summary the information from the nodes set
Set2vec encoder function
Author randomly permutate of the node’s neighbors on an unordered set and feed to the LSTM
HDGI Learning
Mutual information based discriminator
Belghazi et al. proved that the KL-divergence admits the Donsker-Varadhan representation and the f-divergence representation as dual representations:
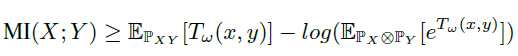
$\mathbb{P}_{xy}$ is the joint distribution and $\mathbb{P}_x\otimes \mathbb{P}_Y$ is the product of margins, $T_w$ is a deep neural network based discriminator.
Author estimate and maximize the mutual information by training an discriminator $D$ to distinguish positive sample set $Pos={[\vec{hn},\vec{s}]}^N{n=1}$ with negative sample set $Neg={[\vec{ \widetilde{hm}},\vec{s}]}^M{m=1}$.
The sample $(\vec{h_i},\vec{s})$ is the positive node belongs to graph, and $(\vec{ \widetilde{h_m}},\vec{s})$ is the generated fake node.
The discriminator $D$ is a bilinear layer:
Loss function:
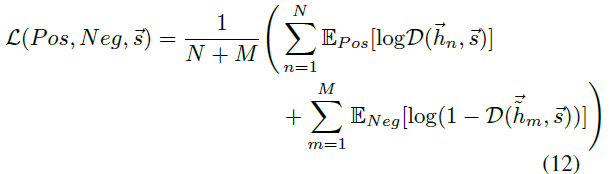
Negative samples generator:
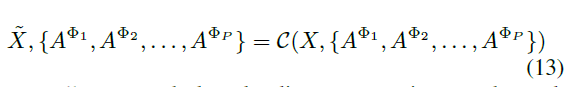
Keep the graph structure unchanged and shuffle the feature of each node in the graph.
Experiment
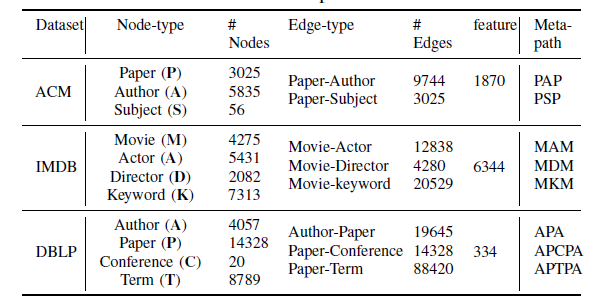
Dataset:
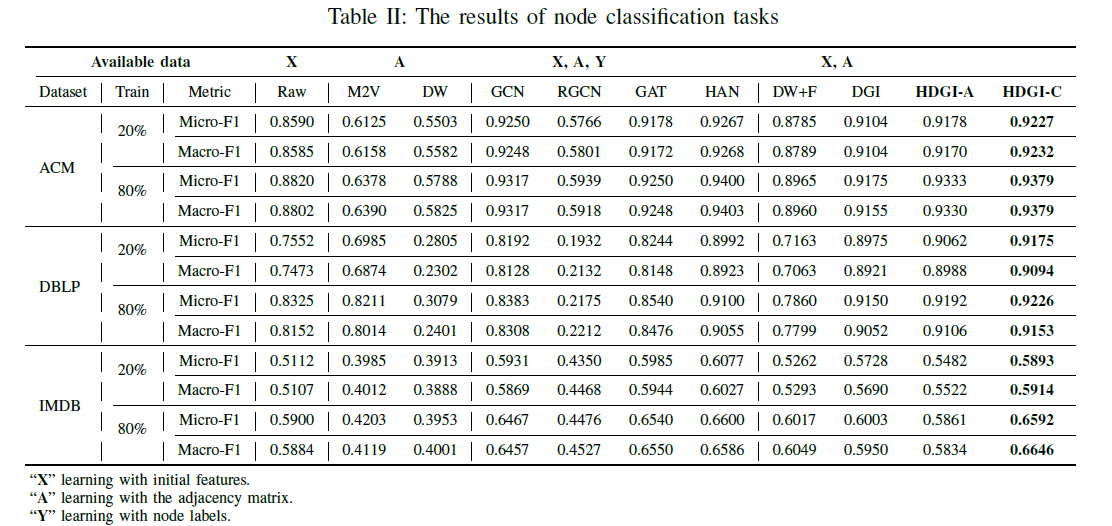
Node classification
Node clustering task
Ablation experiment
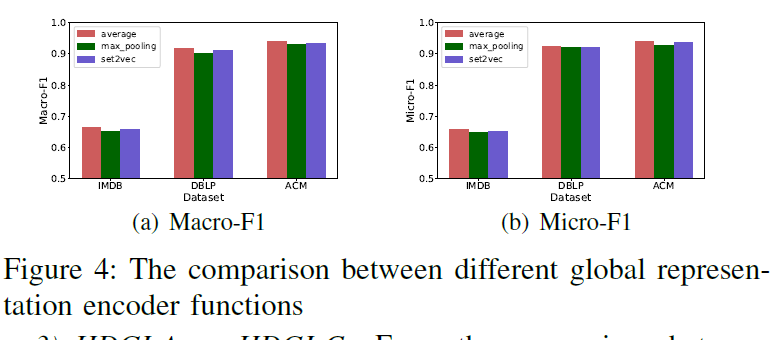
Some discovery :
The HDGI is highly depend on the initial feature $X$, when the $X$ is random initiated the performance of HDGI decreased dramatically.
| Method | Classification (feat) | Classification (no feat) | Cluster (feat) | Cluster (no feat) | ||||
|---|---|---|---|---|---|---|---|---|
| Micro F1 | Macro F1 | Micro F1 | Macro F1 | NMI | ARI | NMI | ARI | |
| HAN | 0.9329 | 0.9336 | 0.8547 | 0.8506 | 0.2691 | 0.2193 | 0.6305 | 0.6956 |
| HGT | 0.8224 | 0.8175 | 0.8298 | 0.8265 | 0.4944 | 0.4782 | 0.4548 | 0.4104 |
| HDGI-C | 0.8273 | 0.8156 | 0.4969 | 0.2246 | 0.0056 | 0.0038 | 0.0202 | 0.0530 |