Motivation
- 现有模型不好解决异构图
- 现有异构图方法缺少理论分析
Intro写作思路:
先介绍GNN以及GNN对应的理论研究,从而过渡到现有GNN模型不能解决异构图问题。(对应背景和现在的工作进度)
接下来介绍现有异构图的问题
- 现有异构图需要人工指定metapath,或者其他需要经验得到的东西。
- 缺少针对HGNN理论分析。
引出本文的核心:Graph Kernel(为什么这里不放在开头呢?因为这个东西是用来解决问题的方法,而不是问题核心。问题还是GNN,所以第一段讲的是GNN)
- Graph Kernel(GK):用于评价图上两个点或者两个子结构之间相似度的东西。(一种算子)
- GK在同构图上的应用,但是在异构图上应用仍然存在挑战(存在什么挑战?这里讲一下是不是好一点。)
本文的工作
Contribution
- 提出了一个基于异构图的Graph Kernel。第一个将马氏距离(Mahalanobis distance,MD)和异构图kernel相结合,来捕获异构信息。
- 通过理论把graph kernel和传统的HGNN联系起来,对传统的HGNN进行了理论分析。
Approach
Graph Kernels
Kernels 把数据映射到一个高纬度空间中,从而可以在高维空间对数据进行相似度计算。
Graph Kernels通过把图分解成不同的子结构,从而进行相似度计算。

当不考虑子结构的时候,Graph Kernel可以只考虑节点的情况

Random Walk Graph Kernel
比较两个图中,长度为l的randomwalk序列的相似度。

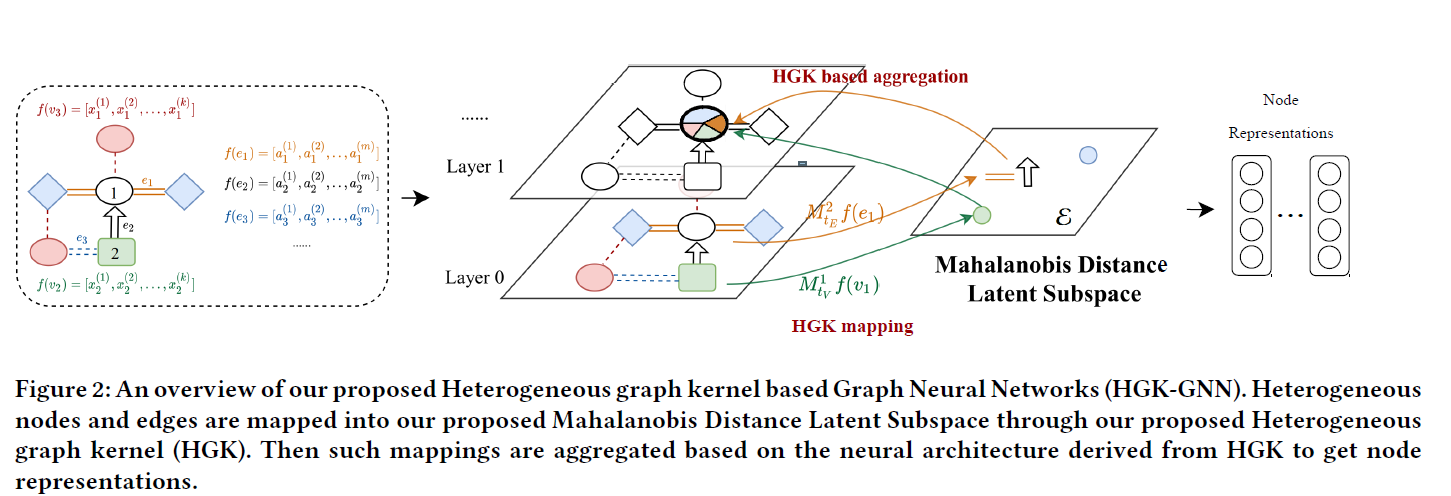
HGK-GNN
Incorporating Heterogeneous Edges.

计算两个节点u,v的相似度,定义Kernel如下:
- 对节点u,v分别用其本身的特征做点乘。
- 同时对其所有的一跳邻居的边的进行组合并交叉相乘(计算量好大)
Incorporating Heterogeneous Nodes
通过考虑不同节点类型和边类型,把不同节点类型节点通过映射函数映射到各自的空间。

对于l层的邻居来说,其graph kernal可以定义成l-1层的邻居相似度乘以l层的邻居+边的相似度。

From HGK to Neural Architectures
从Heterogeneous Graph Kernel到神经网络的表示形式

作者证明得到,在第l层的图神经网络得到的向量表示正好都是对应l层的马氏空间中的向量。

THEORETICAL ANALYSIS
作者接下来了理论分析了HGK-GNN和metapath-GNN的关系
传统的MP-GNN可以表示成用metapath进行聚合的图神经网络

假设当前MPGNN的形式如下

作者证明,在参数如下形式时,HGK-GNN和MPGNN等价