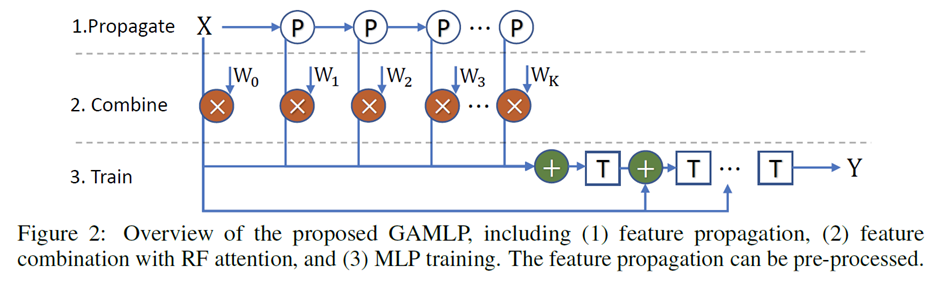
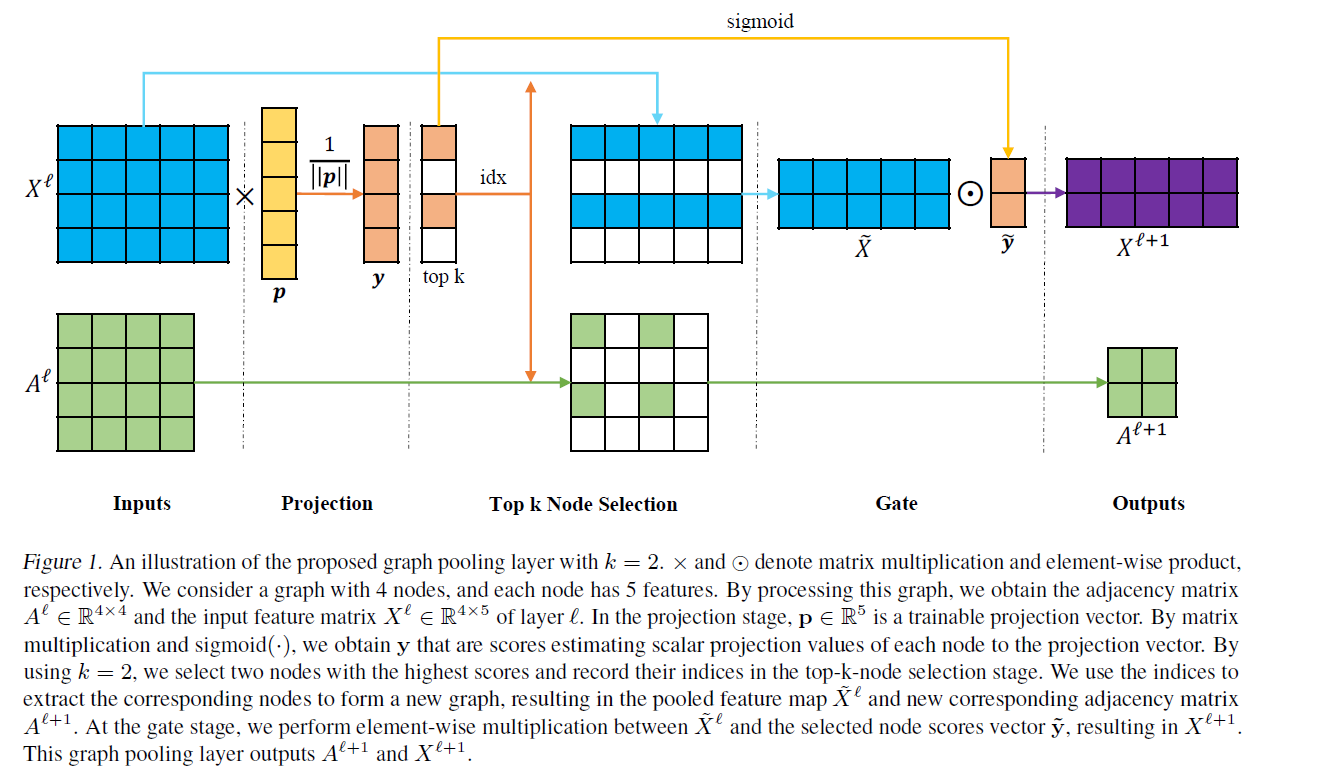
背景
在现在的图卷积中,由于图的大小可能非常大,传统的在全图上进行图卷积的操作往往是不现实的。因此往往采用了图采样的方法。图采样大致会分为:Layer Sampling 和 Graph Sampling两种。但是这两种方法都存在着一些问题。
Layer Sampling:
1. 邻居爆炸:在矩阵采样多层时,假设每层采样n个邻居,则会导致$n^2$级别的节点扩充速度。
2. 领接矩阵稀疏:在矩阵采样的过程中,会导致邻接矩阵稀疏化,丢失一些本来存在的边。
3. 时间耗费高:每一层卷积都要采样,这就导致计算的时间耗费。
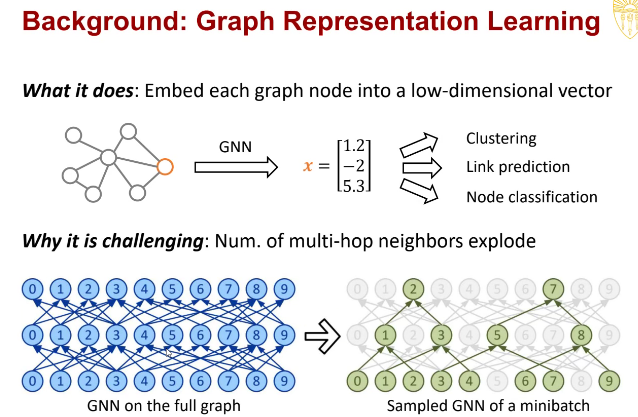
Graph Sampling:
Graph Sampling是一种相对好的采样方法,可以在preprocess阶段提前采样图,并且可以进行mini batch的加速。但是这样的采样往往会丢失一些信息。
本文为了解决以上问题,提出了一种在图上进行Graph Sampling的相对较好的方法。
方法
在普通的Layer采样过程中,我们希望采样之后产生的偏差最小。这个偏差可以由如下的公式得出。
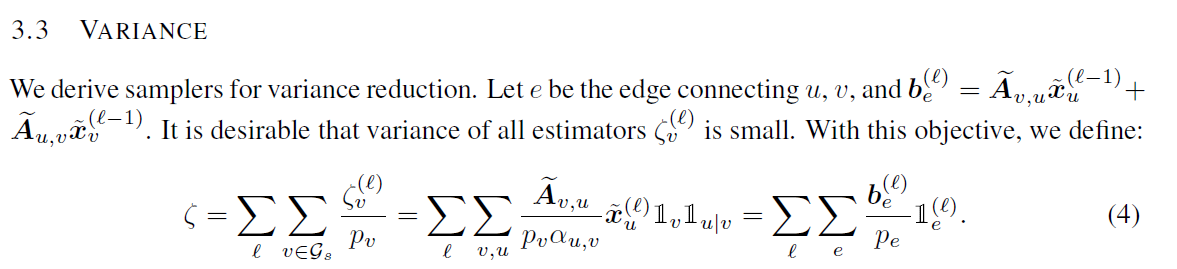
我们希望如下的偏差最小,经过一系列复制的推导,在$P_e$等于如下值的时候,偏差达到最小。

但是此种方法计算需要所有子图中边两端的聚合信息来求得计算量十分大,于是作者采用了如下的简化公式
边的采样概率等于两个节点的倒数之和,来进行Graph的采样
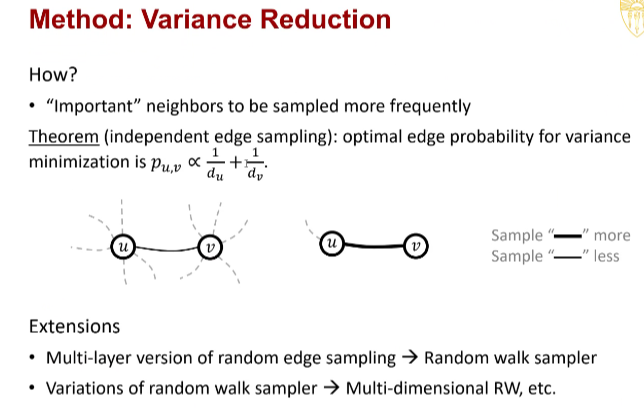

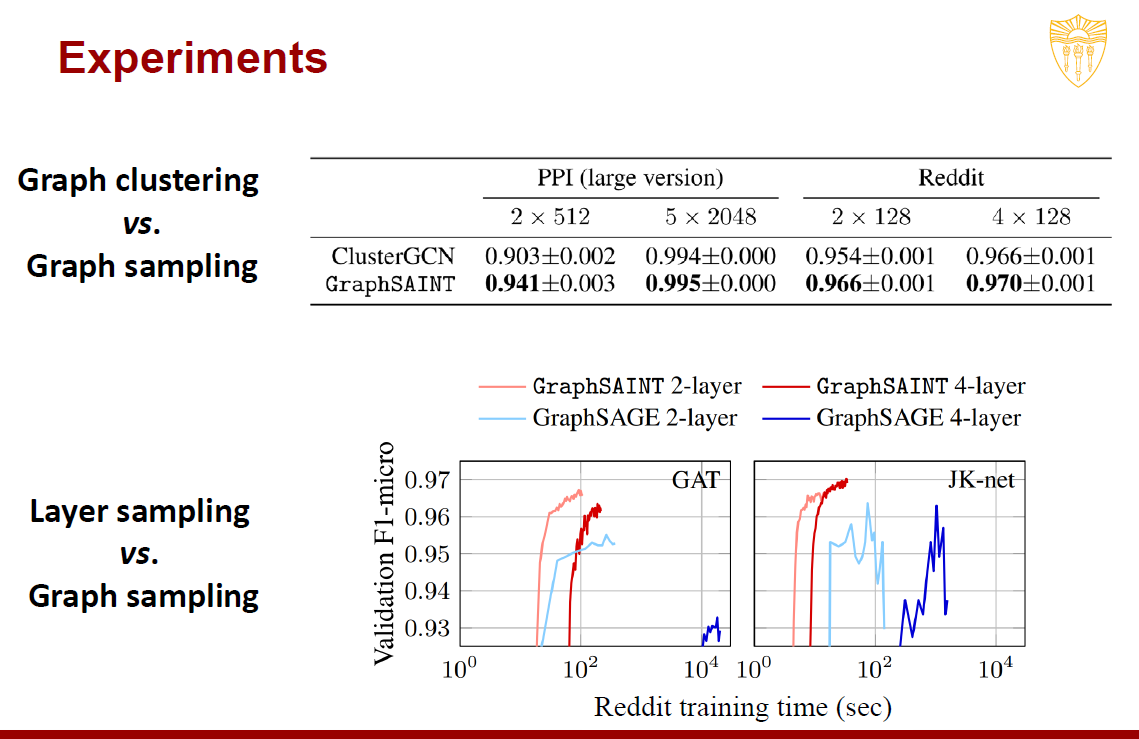
实验
在许多的大图中进行证明,不仅训练速度得到了优化,其准确率也有了提高。
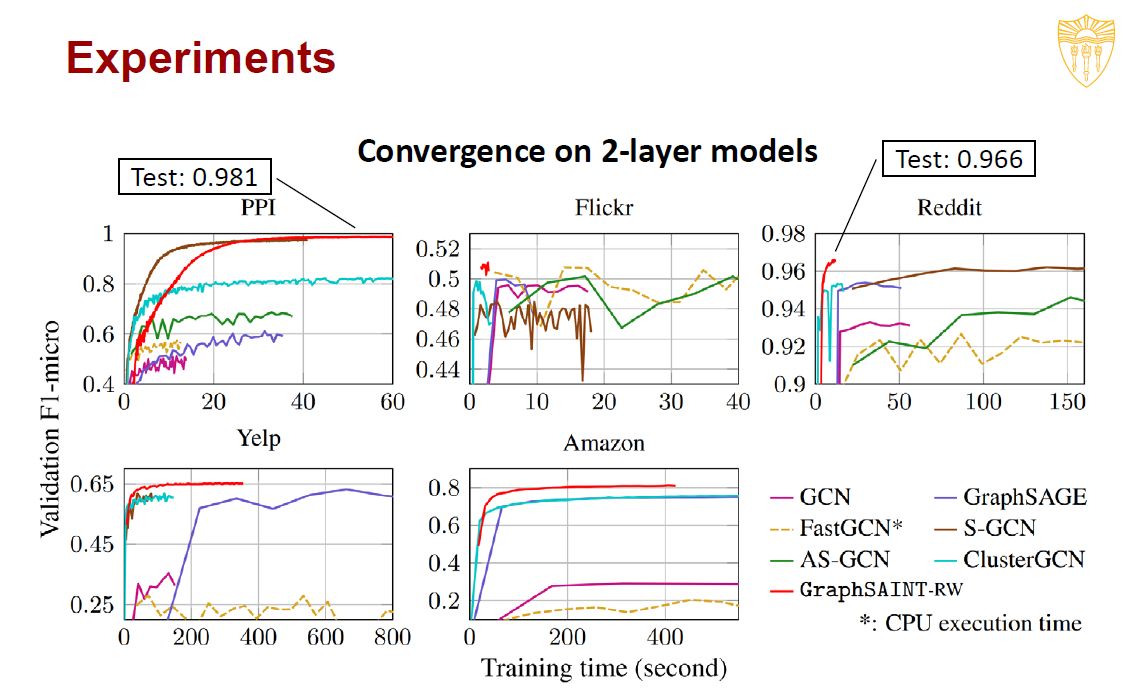
同时对比了Layer Sampling和Graph Sampling,证明了Graph Sampling在多层的时效果有一定的提高